HZNUCTF2024

ez_encode

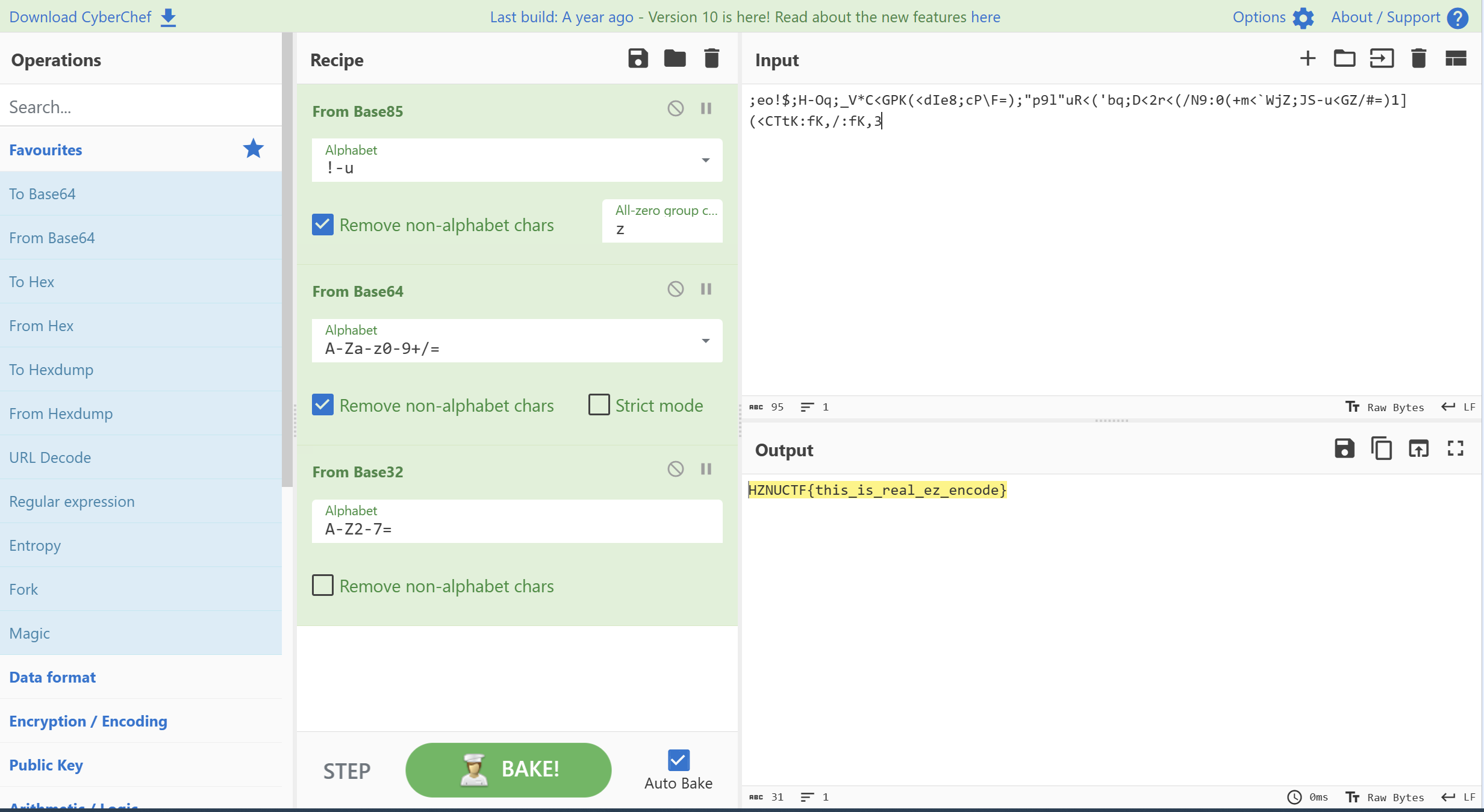
cyberchef 一把嗦了

image-20240414204833256

sign-up

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from gmpy2 import *
from Crypto.Util.number import *
from secret import flag

p=getPrime(1024)
q=next_prime(p+(p>>500))

e=0x10001

n=p*q

c=pow(bytes_to_long(flag),e,n)

print("n=",n)
print("c=",c)

其中q=next_prime(p+(p>>500))指的是：$ q= [p+\frac{1}{2^{500}}p] +r $

即 $ q = [(1+\frac{1}{2^{500}}p] +r $, r是为了将q凑为质数的整数。

$ \therefore n = p\ast q = [(1+ \frac{1}{2^{500}})p^2]+rp$

$ \therefore (1+\frac{1}{2^{500}})n = ((1+ \frac{1}{2^{500}})p)^2 + (1+\frac{1}{2^{500}})rp > ((1+\frac{1}{2^{500}})p)^2 ——①$

∵q2=[(1+12500)p+r]2=((1+12500)p)2+2[(1+12500)rp]+r2——②\because q^2 = [(1+\frac{1}{2^{500}})p + r]^2 = ((1+\frac{1}{2^{500}})p)^2 + 2[(1+\frac{1}{2^{500}})rp] + r^2 ——②

易知，②式大于①式

∴经过比较得[(1+12500)p]2<[(1+12500)n]<[(1+12500)p+r]2\therefore 经过比较得 [(1+\frac{1}{2^{500}})p]^2 < [(1+\frac{1}{2^{500}})n]< [(1+\frac{1}{2^{500}})p + r]^2

通过开方缩小范围得

$(1+\frac{1}{2^{500}})p < \sqrt{(1 + \frac{1}{2^{500}})n} < (1+\frac{1}{2^{500}})p +r = q $

所以，(1+12500)n\sqrt{(1+\frac{1}{2^{500}})n}的下一个素数即为q

q = next_prime(iroot((n + (n >> 500)), 2)[0])

ez_rsa

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from Crypto.Util.number import *
from flag import flag

def keygen(nbit = 32):
	while True:
		k = getRandomNBitInteger(nbit)
		p = 3*k**17 + 3*k**11 - 53*k**7 + 12*k**5 - 114*k + 27329
		q = 5*k**13 - 7*k**11 + 43*k**5 - 313*k**3 - 14*k + 18869
		if isPrime(p) and isPrime(q):
			return p, q

def encrypt(msg, n, e = 65537):
	m = bytes_to_long(msg)
	return pow(m, e, n)

p, q = keygen()
n = p * q
enc = encrypt(flag, n)
print(f'n = {n}')
print(f'enc = {enc}')

根据题目得到一个关于k的多项式方程组

用sage求解多项式

1
2
3
4
5
6
7
var('k')
p = 3*k**17 + 3*k**11 - 53*k**7 + 12*k**5 - 114*k + 27329
q = 5*k**13 - 7*k**11 + 43*k**5 - 313*k**3 - 14*k + 18869

eq=p*q==n

solve(eq,[k])

即可求得k，再求得p，q解一般rsa即可

你知道什么叫第二重要极限吗？

a=lim⁡x→0(a1x+a2x+⋯+anxn)nxa = \lim_{x \to 0} (\frac{a_1^x+a_2^x+\cdots+a_n^x}{n})^{\frac{n}{x}}

你知道什么叫做第二重要极限吗？

其中

1
2
3
a_i = [1,9,9,8,4,6,1,9,9,4,8,1,4]   

flag="HZNUCTF{"+md5(res)+"}"

使用在线工具求得极限后md5加密即可