理论基础

格理论的起源可以追溯到 17 世纪有关球堆积问题的研究，直至 1840 年，高
斯才引入格在几何中的概念并给出了三维空间中球的最大堆积密度。格在群论和几何中的定义不同于离散数学中有关偏序集合的描述，几何上，可以将格看作是具有周期性结构的 n 维空间中的点的集合。
Shamir最早将格理论引入密码学领域，其在 1982 年利用格对背包公钥密码体制进行了攻击，后来 Coppersmith对其分析方法做了推广，将破解 RSA 公钥密码体制的问题转化成了求格中的困难问题。近些年，随着对格理论中有关计算性难题的研究，人们发现其在数论、计算机科学、密码分析和设计中都有着很广泛的应用前景。*

格的定义

设$b_1,b_2,…,b_n\in \mathbb{R}^m$一组线性无关的向量，其产生的格被定义为

$L(b_1,b_2,...,b_n) = \{ \Sigma^n_{i=1}x_ib_i|x_i\in\mathbb{Z}\}$

简记为L，m为格L的维数，n为格L的秩，通常研究满秩格，即m=n。称$B={b_1,b_2,..,b_n}$为一组格基，同一个格L可以由不同的格基来表示。

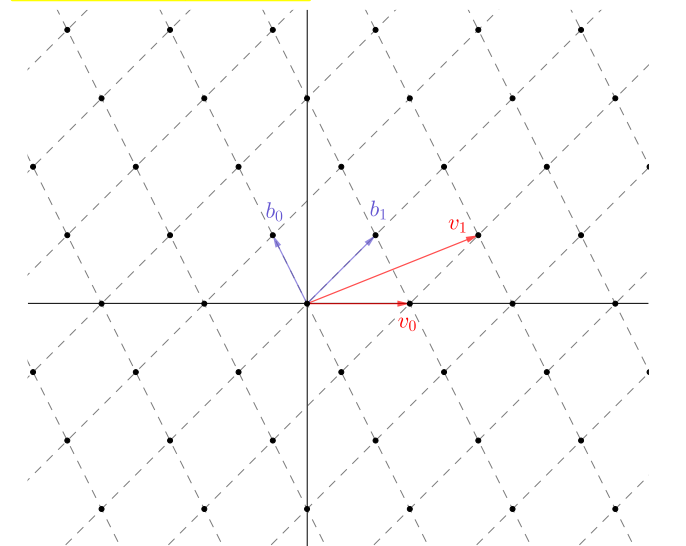
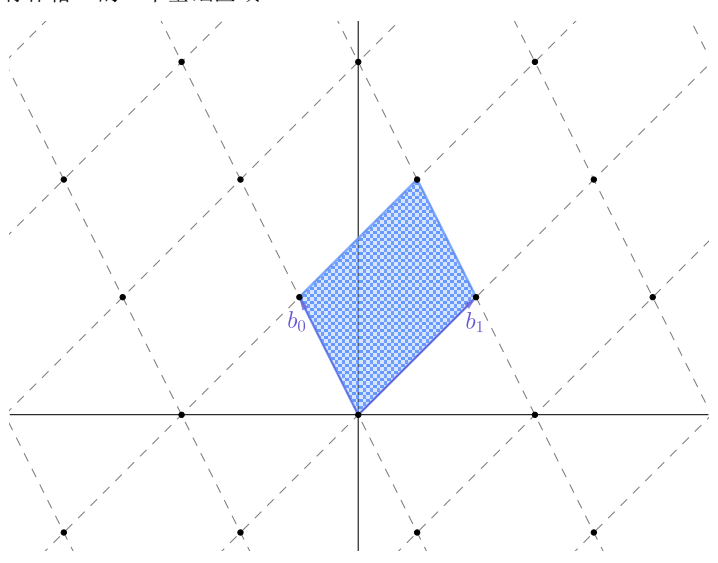
上图展示了由基向量${b_0,b_1}$或${v_0,v_1}$生成的二维格。

在给定格L中的任意一组基向量，将其以行向量的形式表达为矩阵A，通过对A左乘一个幺模矩阵$U\neq I$（如果$A \in R ^{m\times n}$是整数矩阵，r=rank(A)=min{m,n}而且A的所有非零rxr子式等于1或-1，则称A为幺模矩阵）得到矩阵UA，UA的行向量则表示格L的另外一组基。

一般来说，如果一组基向量几乎是正交的，那么认为它是好的基向量，否则认为是坏的。如上图，${b_0,b_1}$是一组好的基向量，${v_0,v_1}$是一组坏的基向量，基向量正交的程度直接影响解决格问题的复杂程度。

格的延展空间

设n维格L(B),其基向量B的所有线性组合形成的集合

$span(B) = \{Bx|x\in \mathbb{R}^n \}$

称为这组基向量的延展空间

格的延展空间为整个n维空间的前提是为满秩格

格的基本空间

设n维格L(B),以下向量的集合

$P(B) = \{Bx|x\in\mathbb{R}^n,\forall i:0\le x_i\le1\}$

称为格L的一个基础区域。