纠错码理论

​ 纠错码一开始应用于数字通信系统，目的是使消息可以在信道中可靠的传输而不产生错误，其通过在消息中增加冗余的方法，排除噪声信道下带来的干扰，从而使接收方能够正确的检测或纠正错误

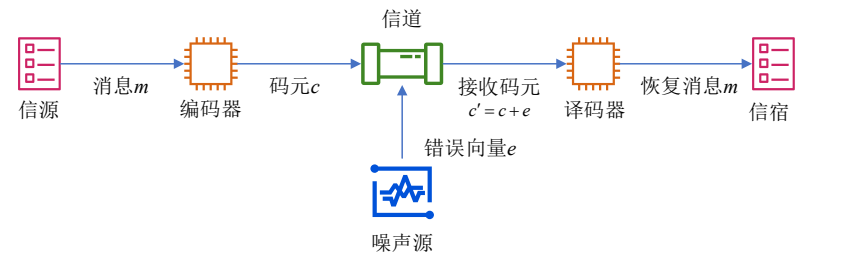
image-20240407195159132

分类：

  • 线性分组码
  • 线性卷积码
  • 非线性卷积码等

密码学中常用线性分组码

定义1（线性分组码）：

二进制(n, k)线性分组码 C 是 GF(2)上的 n 维线性空间的一个 k 维子空间。n 表示码字的长度，k 表示消息位的长度。

定义2 （生成矩阵，校验矩阵）:

对于(n, k)线性分组码 C，对于(n, k)线性分组码 C，若矩阵$G \in F_2^{k \times n}$满足

称矩阵G为码C的生成矩阵。

可见，码字空间是矩阵G的行的线性组合张成的子空间，对G做初等变换有$G=[I_kP]$,$I_k$是k阶的单位阵，P是大小为$k\times (n-k)$的矩阵，由该G生成的码称为系统码，且系统码的前k位是信息位，后$(n-k)$位是校验位。

若矩阵$H \in F_2^{(n-k)\times n}$满足

称矩阵H为码C的校验矩阵

定义3 （校验子）：

设向量$c\in F_2^n$,校验矩阵$H\in F_2^{(n-k)\times n}$。若向量$s\in F_2^{n-k}$有

称s为向量c的校验子。当码字正确是，校验子为0向量。

定义4 （汉明重量）：

设向量$c\in F_2^{n}$,汉明重量指向量中非0元素的个数，记作$w(c)$

定义5 （汉明距离）：

设向量$a,b \in F_2^n$,汉明距离指对应位置不同元素的个数，记作$d(a,b)=w(a-b)$

定义6 （最小距离）：

设线性分段码C，$\forall c1,c_2\in C$且$c_1 \neq c_2$，最小距离记作$d{min}= min\ d(c1,c_2)$。其等价于线性分组码C中非零码字的最小汉明重量，即$c\in C,c\neq0,d{min} = min\ w(c)$。

若一个(n,k)线性分组码的最小距离为$d_{min}$，则

  1. 检测出e个随机错误，需满足$d_{min}\ge e+1$

  2. 纠正出t个随机错误，需满足$d_{min} \ge 2t +1$

  3. 纠正出t个随机错误，且检测出e个随机错误，其中$e \ge t$，需满足$d_{min} \ge e+t+1$

下文将以(n,k,d)表示线性分组码，其中d表示$d_{min}$

定义7 （等价类）：

设(n,k,d)线性分组码$C_1$和$C_2$，置换$C_1$中的n个码元位置并加一个不变的n维向量a后能够得到$C_2$，称$C_1$与$C_2$属于一个等价类。即

对$C_1$和$C_2$而言，判断二者是否为同一等价类等价于寻找k阶满秩方阵S和n阶置换矩阵P，使得$C_1$的生成矩阵$G_1$和$C_2$的生成矩阵$G_2$满足

若满足上式，则代表$C_1$与$C_2$等价。